3.1. The interactive calculator¶
We start (preferably on jupyter notebook) importing the module and creating our cosmology object:
Only the label of the model is really needed here, since the essentials
are already predefined in the program, as mentioned above. With this,
one can explore the properties assigned to the object. For example,
LCDM.model will print lcdm. LCDM.species is a dictionary of
Fluid objects identified by the components labels, in this case
cdm and lambda. There is also a dedicated class for an
equation-of-state parameter or function, which becomes an attribute of
its fluid. We can assess its value, type, etc.
LCDM.species['lambda'].EoS.value will print -1.
But let us proceed in a slightly different way, setting up our model
with some options. Since we predominantly work with flat cosmologies (in
fact, curvature is not supported yet in the current version), the
flatness condition is imposed in the density parameter of one of the
fluids. We will choose the dark energy density parameter to be the
derived parameter, but we could have chosen dark matter as well. Also,
by default, the code prefers to work with physical densities (for
example \(\Omega_{c0} h^2\)) rather than the common
\(\Omega_{c0}\). You can change this with the option
physical=False. We will add the radiation and matter fluids. Note
that this will override the optional inclusion of baryons and remove
them, if given. The radiation fluid is parametrized by the temperature
of the cosmic microwave background. The model will have three free
parameters: the physical density parameter of matter
(\(\Omega_{m0}h^2\)), the CMB temperature (\(T_{\gamma}\), which
we usually keep fixed) and the Hubble parameter \(h\); and one
derived parameter, which is the density parameter of the cosmological
constant, \(\Omega_{\Lambda}h^2\).
We can then obtain the solution to the background cosmology with EPIC.
Solving the background cosmology¶
It is as simple as this:
Normally, a set of parameters would be given to this function in the
form of a dictionary with the parameters’ labels as keys, like in
parameter_space={'Oc0': 0.26, 'Ob0': 0.048, 'Or0':8e-5, 'H0':67.8}.
However, we can also ommit it and turn on the option accepts_default
and then the default values defined in the
EPIC/cosmology/default_parameter_values.ini file will be used for
the parameters. Next, we plot the energy densities and density
parameters. Here I do it in a jupyter notebook with the help of this
simple function below:
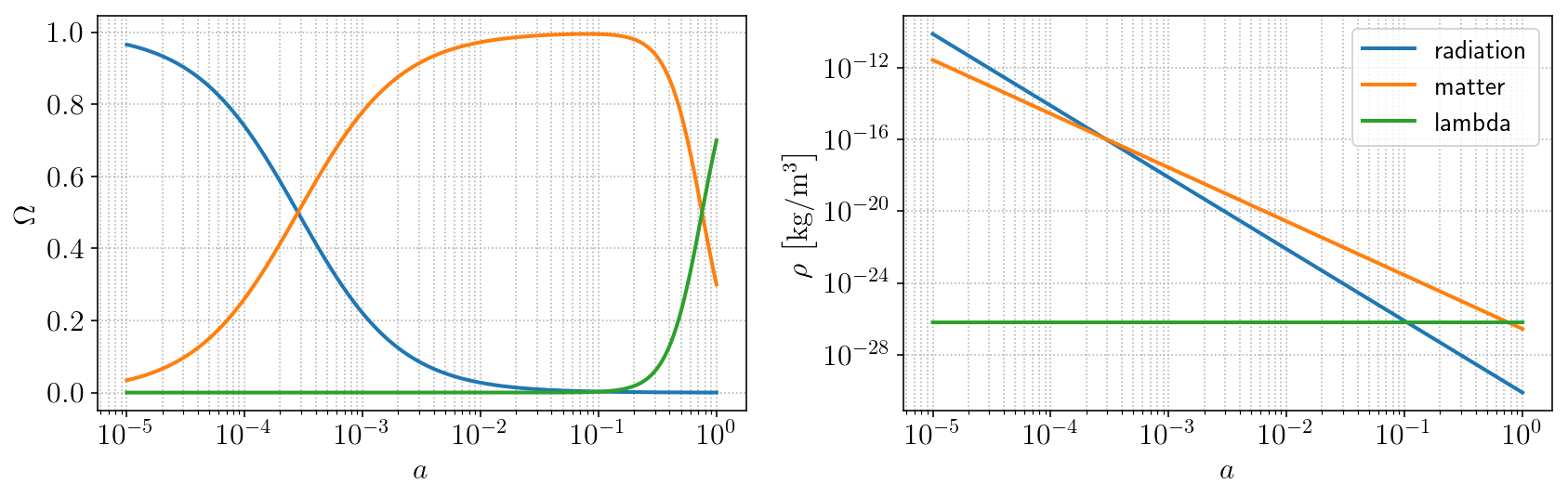
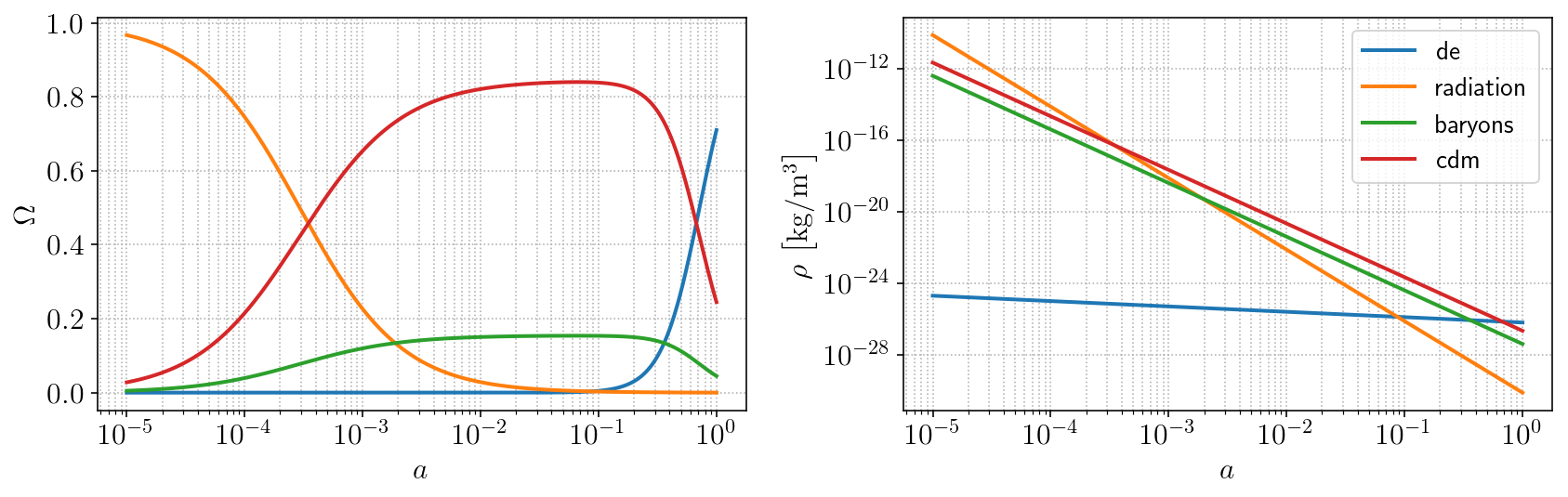
Notice the matter-radiation equality moment at
\(a_{eq} \sim 3 \times 10^{-4}\) and the cosmological constant that
just recently came to overtake matter as the dominant component. The
\(w\text{CDM}\) (wcdm) model differs from
\(\Lambda\text{CDM}\) only by the dark energy (de)
equation-of-state parameter (wd), which although still constant can
be different from \(-1\). Note that the energy density of dark
energy is not constant now: